Let's Talk Worst Case Tolerance Analysis

Worst Case Tolerance Analysis is important to many industries. Used for critical measures, Worst Case has an important place in tolerance analysis.

Part 4: 3DCS V7.5 – 3DCS V7.5 – How and Why to Use Worst Case Analysis in 3DCS

Thu, Apr 26, 2018 11:00 AM - 12:00 PM EDT -- Learn how to handle Worst Case

How does 3DCS handle Worst Case?

Let's first review what Worst Case is in this context.

Worst Case Tolerance Analysis

Worst Case Tolerance Analysis is a traditional method of performing a stack up calculation. It derives from setting all of the tolerances at their limits in order to make a measurement the largest or smallest possible by design.

This process doesn't use statistical probability and instead focuses on whether or not the product falls within its specification limits.

Therefore, the Worst Case Model is intended to predict the maximum expected variation of a given measurement. The goal is to design to this maximum to guarantee that 100 percent of the parts manufactured will assemble and function properly.

However, in reality, this is rarely the final outcome.

Designing to Worst Case can require extremely tight tolerances that may require expensive manufacturing and inspection processes to produce. This can drive up the cost of the parts, and increase scrap rates.

In most cases, a statistical analysis can deliver the necessary, and reliable, results needed to design to specification while lower costs by focusing on key areas to quality. That's a bold claim, though, so how do we back it up?

Statistical Variation Analysis

Statistical Variation Analysis, most often using a Monte Carlo Method, uses statistical probability to determine the percent chance parts will be out of given specification limits. It does so by randomly generating tolerance values within the given range for each tolerance in the model. It does so for hundreds and thousands of models, and then computes the statistical results of all of those random model builds together. Using the Monte Carlo Method, the default analysis isn't a true random distribution, but instead a standardized distribution that results in more tolerances being near the mean (unless a different distribution is selected!).

An alternative method uses a RSS three-dimensional stack-up analysis to determine the overall variation. This method (referred to as GeoFactor in 3DCS), is less reliable than a Monte Carlo Method for all cases, but provides additional insight into your model.

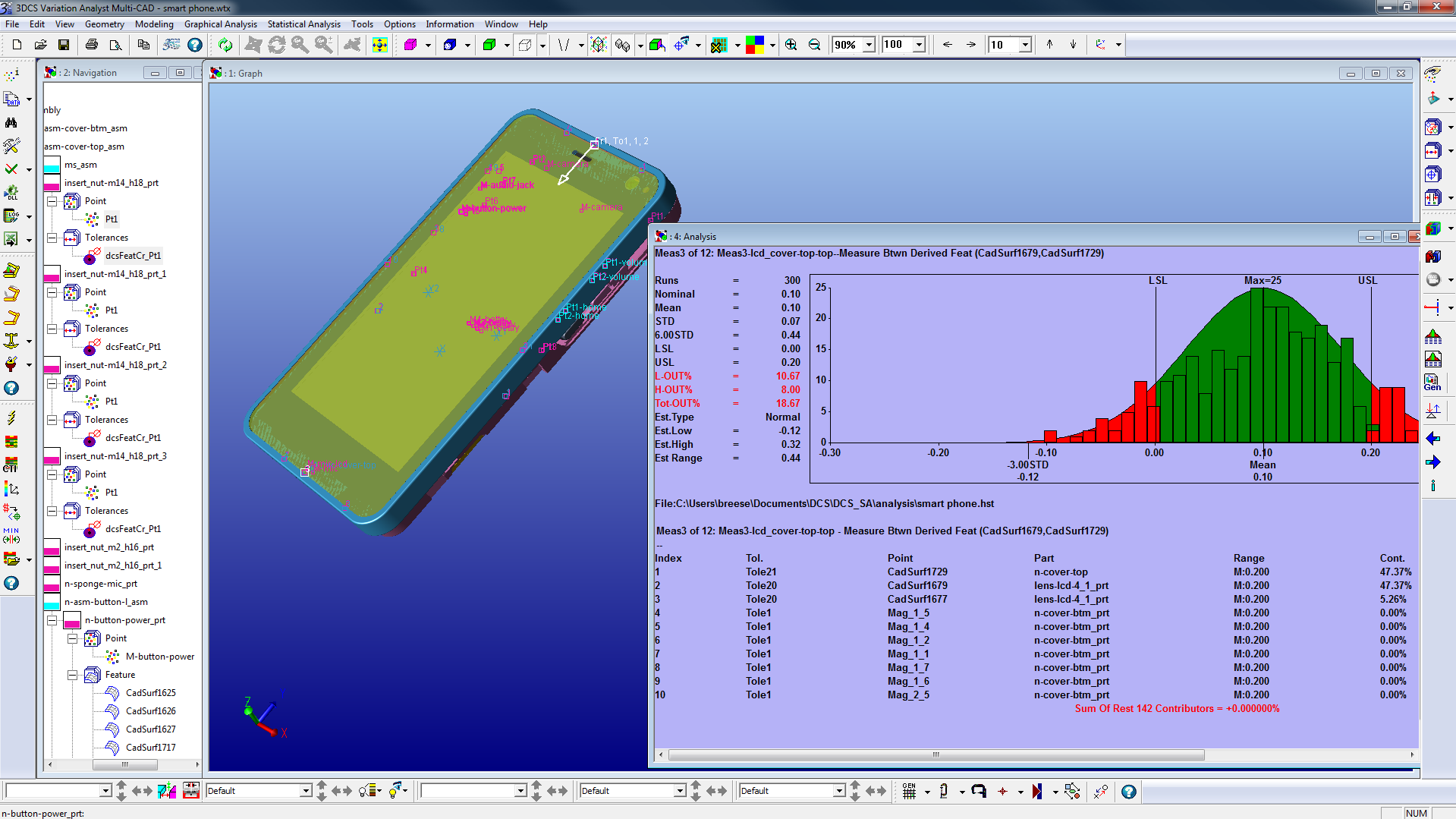
analysis of 3DCS measurement

With a statistical method, there are a number of value-add's:

1. Design to a given quality level, not just 100%

2. Loosen non-critical tolerances (and thereby reduce manufacturing costs)

3. Find critical tolerances to quality for focus and measurement planning

4. Test design scenarios and solutions digitally

3DCS Take on Worst Case - True Worst Case Scenario

3DCS users are not just interested in a total stack up of tolerance maximums and minimums, but in a true 'Worst Case Scenario'. What this means is, rather than simply set all tolerances to their maximums or minimums, 3DCS simulates the tolerances in either direction, and compiles the results in a three dimensional stack. It then checks the results, for each measurement, to find what combination of maximum and minimum tolerances cause the highest level of out-of-specification scenario, i.e. what is the worst possible combination of tolerance deviations that can occur?

Random “Worst Case” - How Does 3DCS Calculate Worst Case

One common way of running a “Worst Case” study in 3DCS involves the use of a dynamic linked library dcu_simu_fn.dll, and the routine dcsSimuWorstCase. The technique simply changes all the magnitude tolerances in the model to Modal distribution so the Monte Carlo simulation uses the extremes of the tolerance ranges.

NOTE: Do not try this at home! If you try this DLL on your own, always remember to SAVE before activating it, as it can modify all of the features in your model!

The Modal distribution makes it much more likely to hit the extreme minimum and maximum combination of tolerances for each of the measurements. Even so, many samples need to be run particularly for larger models with positional tolerances, i.e. tolerances that are dependent on angular variations.