
It is often applied to manufactured parts in general to determine the impact of manufacturing processes on the final dimensions of those parts. Tolerances are determined by a variety of methods, from standards such as ISO or ASME, or from the use of geometric dimensioning and tolerancing (GD&T), a method of annotating and marking tolerances on parts.
Traditional methods of tolerance analysis include 1D, 2D and 3D Tolerance Stacks, and statistical methods like Monte Carlo simulations. Tolerance Stacks calculate the accumulated variation across a set of dimensions. 1D stacks do a single directional linear stack, while 2D stacks and 3D stacks include multiple directions and influencers.
As we discussed in our article, What is Tolerance Analysis?, there are really four different methods of doing Stack Analysis -
It is important to account for manufacturing variation, as there is no such thing as perfect parts. What's more, those tolerances and variation can greatly affect production costs.
When manufactured, parts are never made to perfect specifications. Due to variation caused by material characteristics and manufacturing processes, such as stamping and machining, parts are always made larger or smaller than their nominal design. This variation is captured in design as tolerances, depicting the range of variation acceptable in the design.
Tolerancing directly influences the cost and performance of a product. A piece of sheet metal that is quickly stamped using a stamping die is much cheaper to produce than one that needs to be machined to more precise dimensions. The same applies for plastics, composites and any given part. The tighter, as in the smaller, the tolerance, the more difficult the part is to produce, and the more expensive the part is. In the same regard, the performance of a part and product is influenced by tolerances. An automobile door will not close well if the tolerances are very large, and may have additional road noise from a poor seal. Aircraft wings may need large amounts of shims if the tolerances are incorrect in order to fit properly to the fuselage. This costs time, money and increases the weight of the aircraft, reducing its fuel efficiency.
Therefore, tolerancing and tolerance analysis are integral parts of the engineering process and product lifecycle management in order to produce high-quality products at reasonable prices.
The main issue in Tolerance Analysis is how to calculate the total variation from accumulating tolerances. There are two major categories in this area:
(a) Worstcase Analysis; and
(b) Statistical Analysis.
Let Ms be an output, Ms0 be the nominal value, λsi (i = 1, 2, … Nt) be the constant parameter, Ti be the tolerance, and Nt is the total number of tolerances.
Let T = [T1, T2, …, Tnt] t .
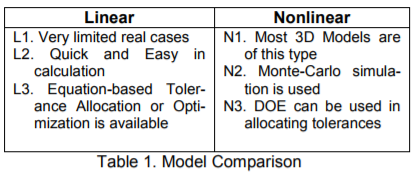
A Linear Model can be represented as Ms = Ms0 + ∑(λsiTi) (eq1)
A Nonlinear Model can be presented as Ms = f(T) (eq2) Where f() is a nonlinear function.
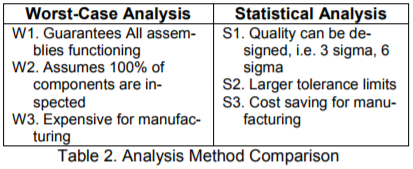
Worst-case tolerance analysis is the traditional type of tolerance stackup calculation. Each tolerance is set to its largest or smallest limit in its total tolerance range. This does not consider the distribution of tolerance range, only that each tolerance stays within its expected range. This method does guarantee that that the parts will fit and function properly, regardless of actual variation. However, because this method often requires very tight individual component tolerances, as the total stack up at maximum conditions is the primary attribute used in the design, it promotes expensive manufacturing and inspection process and high scrap rates.
This method is often requested by customers for critical interfaces in assemblies, but as mentioned, suffers from over-tolerancing parts. The worst-case scenario rarely if ever occurs in actual production, and therefore often incurs unnecessary costs in manufacturing and quality.
A well performed statisitical method can reduce the manufacturing costs by accounting for acceptable levels of variation, designing what is called a Robust Design, which 'loosens' (ie. increases) the tolerances on non-critical areas where it does not affect the overall build, and focus on the critical and sensitive features of the product.
(a1) Linear Case: ∆Ms = ∑(|λsi| ∆Ti) (eq3)
Where ∆Ms is the variation range for the output, and ∆Ti is the variation range for the tolerance Ti.
(a2) Nonlinear Case: ∆Ms = Max{f(T)} – Min{ f(T)} (eq4)
Statisitical Variation Analysis applies statistical controls and methods to relax component tolerances without negatively impacting product quality.
Each part is modeled using a statistical distribution for its tolerance range (variation) which are then summed using the Root Sum Squared method to predict the distribution of the assembly measurements. This process describes the variation as a distribution instead of only showing the extremes of variation, which gives more design flexibility by allowing the design and engineering team to account for varying levels of quality, instead of just 100 percent of all variation, which is statistically rare or impossible.
Tolerance stackups serve engineers by:
(b1) Linear Case with all Normal distributed tolerances: σs 2 = ∑(λsi 2 σti 2 ) (eq5)
Where σs is the standard deviation for the output, and σti is the standard deviation for the tolerance Ti.
(b2) Linear Case with Non-normal tolerances: σs 2 = ∑[λsi 2 sti 2 ] (eq6)
Where sti is the adjusted sigma based on the distribution type for Ti. For example, a uniform distributed tolerance Ti will have sti 2 = (∆Ti 2 /12).
In equation eq6, the calculation is performed based on the Normal approximation for a symmetrical Nonnormal case. It assumes there is no mean shift. A simulation method can also be used as outlined in the following case.
(b3) Nonlinear Case: Monte-Carlo simulation is used to calculate the accumulation as follows:

For a total number Ns of samples, the unbiased standard deviation for the output Ms can be calculated as follows:
σs 2 = 1 1 Ns − ∑= Ns j 1 ( msj – ms ) 2
where,
ms = Ns 1 ∑= Ns j 1 msj.
The following two tables summarize the advantages and disadvantages.
A safety factor is often included in designs because of concerns about:
In most cases, a dimensional variation problem is non-linear relationships in your model.
However, if we consider that tolerances are small relative to dimensions, we can approximate a non-linear relationship with a linear model. Besides the calculation advantage, the sensitivity analysis is also an important reason to have the linearized model (although, there is a coming solution in AAO Add-on for non-linear models; see the webinar at the bottom).
The following are brief descriptions for three linearizing methods - calculating the coefficient λsi in the equation:
Ms = Ms0 + ∑(λsiTi).
(1) HLM method
This method assumes that an output is the sum of individual contributors.
λsi = HLM Indessi(Ti) = RangeMsi(Ti)/∆Ti
Where RangeMsi(Ti) is the contributing value from tolerance Ti; and ∆Ti is the variation range for the tolerance Ti.
(2) Taylor Expansion
λsi = GeoFactorsi(Ti) = [RangeMsi(Ti) / ∆gT] Where ∆gT is the GeoFactor tolerance range.
(3) DOE Method - Design of Experiments
λsi = Coefsi(Ti) = [RangeMsi(Ti) / ∆dTi] Where ∆dTi is the DOE tolerance range.
The coefficient λsi in a linearized model also provides the sensitivity relationship from a tolerance Ti to a measurement Ms.
Learn More About 3DCS Software Here
Click to Learn More About 3DCS With Our Introduction Video Series
These Stories on 3DCS
Comments (1)