3DCS Datum Optimizer (DO) is a tool that uses a genetic algorithm (GA) to determine the optimal datum features from a candidate set with the goal of minimizing the rigid part variation or compliant part deformation. Using DO during the design stage and prior to production gives users the ability to eliminate or minimize rework, reduce tuning mechanisms to select the proper datum features, and have a higher confidence in passing Gage Repeatability and Reproducibility (R&R) studies.
Improper selection of datum features during manufacturing and assembly may cause severe quality problems. Improper datum features risk turning all the quality parts, accurate dimensioning and tolerancing, and first-class operations into a defective assembly.
Datum Optimizer is an easy-to-use tool in 3DCS Advanced Analyzer and Optimizer Add-on, which does not require creating moves (Assembly Definition) or tolerances on the model. For a rigid part, it only requires a single CAD part with a set of candidate points. For a compliant part, besides the part and candidate points, it additionally requires the 3DCS FEA Compliant Modeler Add-on and Finite Element Analysis (FEA) files to be ready as it involves FEA calculations.
Datum Optimizer has two functions in the current version. One is for rigid parts and the other is for compliant parts.
This function finds the three optimal primary datum features to locate a rigid part to a fixture. To achieve this, DO uses a step-plane move, applies a constant ± tolerance on the target locators, and measures point displacements over the part to minimize the variation.
To use this function, the user only needs to select the part, pick a set of points as primary datum candidates, and select desired secondary and tertiary constraint points. DO will find the optimal datum features based on the selected objective function, which is explained later in this paper.
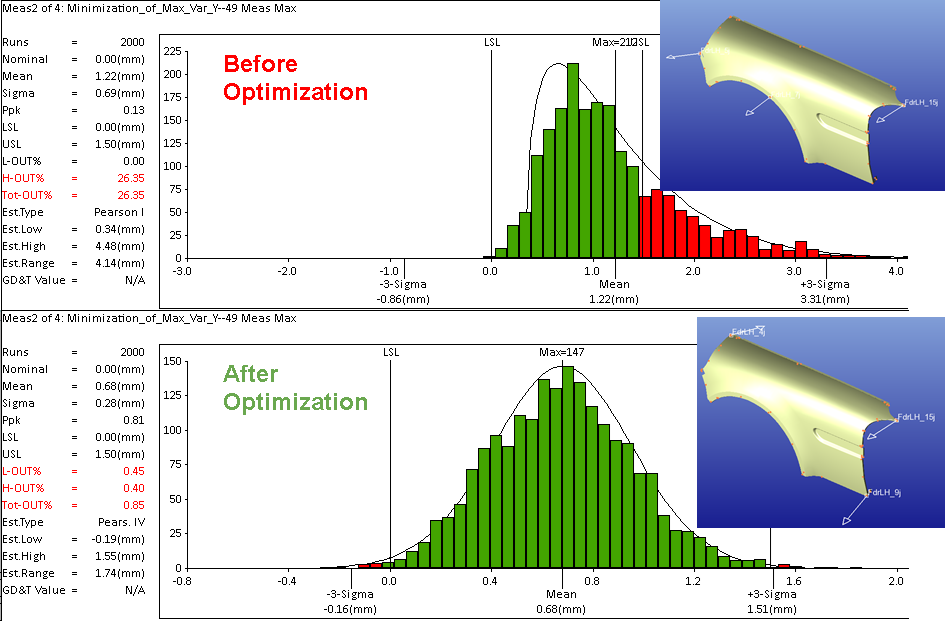
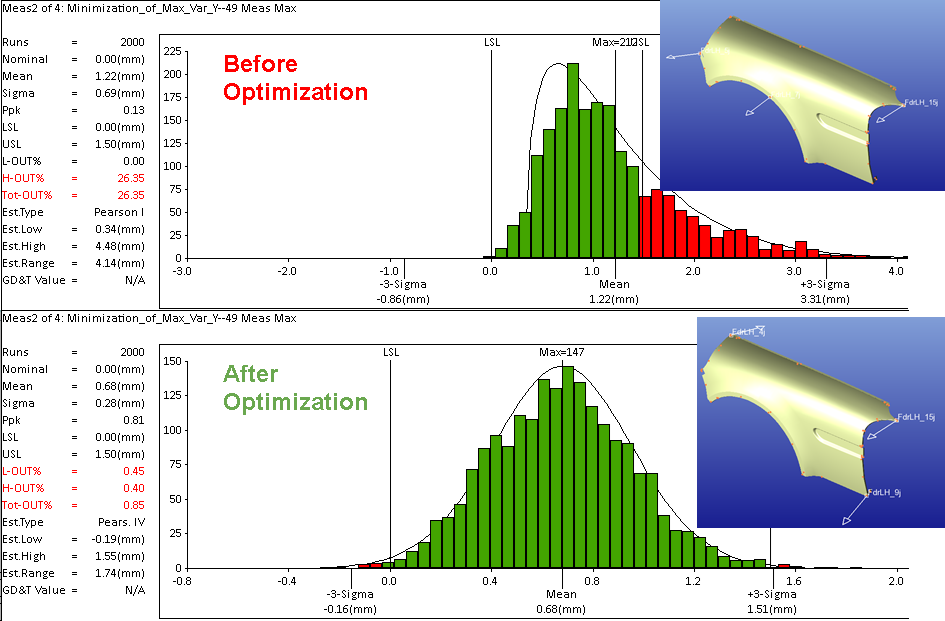
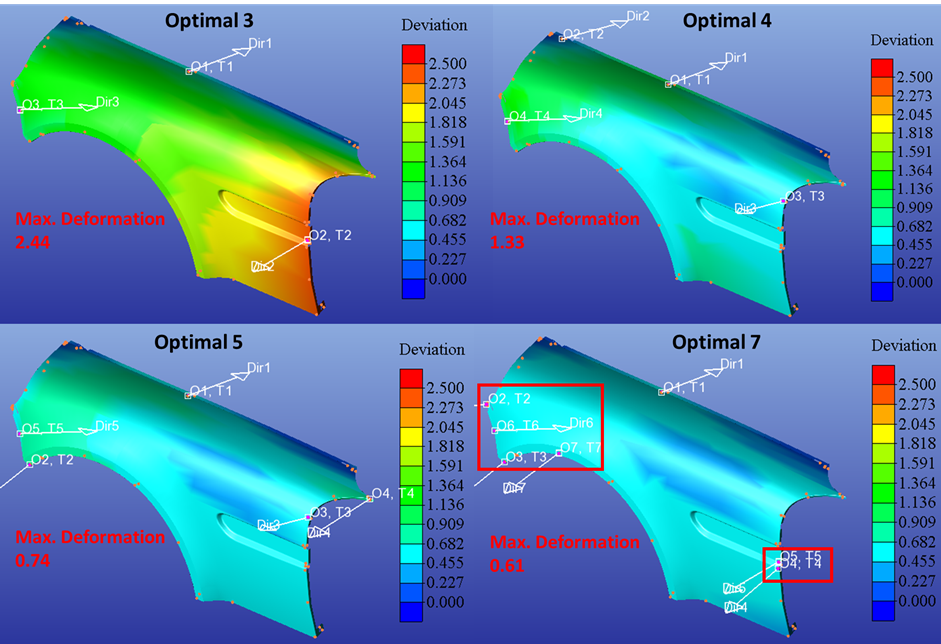
Flexible parts, especially large sheet metal such as automotive hoods or aircraft skins, may need more than a 3:2:1 locating scheme to control the large amount of deformation and pass Gage R&R. However, adding more locators than necessary drives costs up with no significant value add. DO reduces cost by finding the gain-cost relationship in terms of part deformation versus the number of optimal clamps, and provides the minimum number of clamps and locations for the optimal benefit.
To find the optimal clamp locations, DO requires the following: FEA data to be loaded, constrained degrees of freedom (DOFs) for secondary and tertiary points, applied clamps, applied gravity, and measured points for deformation over the part. Datum Optimizer will combine these inputs and provide the best options to minimize the deformation induced by gravity and clamp operation.
It is important to note that there are no tolerances considered in this function.
Datum Optimizer supports two objectives implemented for both rigid and compliant parts. One is minimization of maximum value, and the other one is minimization of average value. Value here represents variation for a rigid part or deformation for a compliant part.
The goal of minimization of maximum value is to guarantee the critical point to satisfy the specification, and the goal of minimization of average value is to satisfy the overall quality. Users should choose one based on their requirements.
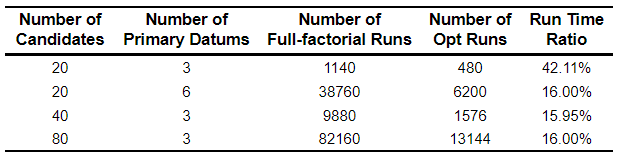
DO has two simulation types - Genetic Algorithm-based optimization or full-factorial simulation. Full-factorial simulation guarantees that users can find global optimal (Best) datum features, but requires more computational resources. The number of possible combinations of n candidates taken r at a time is Cnr =n!/(r!(n-r)!). The number of simulations grows dramatically as the number of candidates and number of datums grows. As shown in Table 1, finding 3 optimal primary datums out of 80 candidates, full-factorial simulation requires 82,160 runs. The Genetic Algorithm-based optimization limits the maximum number of simulations to the population size times the number of generations. With default parameters set, DO only requires 13,144 runs, which is 16% of the full-factorial runs, while having more than a 90% possibility to find the global optimum. This means that you can use only 16% of the computational power to get a 90% chance of success in finding the global optimum. Even though the Genetic Algorithm-based optimization method has an excellent gain-cost ratio, full-factorial simulation is recommended if computational resources are not a concern for you.
Table 1: Comparison of number of runs of full-factorial and Genetic Algorithm-based optimization
No Comments Yet
Let us know what you think